TNL::Solvers::ODE::StaticMerson< Containers::StaticVector< Size_, Real > > Class Template Reference

Solver of ODEs with the first order of accuracy. More...

#include <TNL/Solvers/ODE/StaticMerson.h>

Inheritance diagram for TNL::Solvers::ODE::StaticMerson< Containers::StaticVector< Size_, Real > >:

Collaboration diagram for TNL::Solvers::ODE::StaticMerson< Containers::StaticVector< Size_, Real > >:

Public Types
using	DofVectorType = VectorType
	Alias for type of unknown variable \( x \).
using	IndexType = int
	Type for indexing.
using	RealType = Real
	Type of floating-point arithemtics.
using	VectorType = Containers::StaticVector< Size_, Real >
	Type of unknown variable \( x \).
Public Types inherited from TNL::Solvers::ODE::StaticExplicitSolver< Real, int >
using	IndexType
	Indexing type.
using	RealType
	Type of the floating-point arithmetics or static vector.

Public Member Functions
__cuda_callable__	StaticMerson ()=default
	Default constructor.
__cuda_callable__ const RealType &	getAdaptivity () const
	Getter of the parameter controlling the adaptive choice of the integration time step.
__cuda_callable__ void	setAdaptivity (const RealType &adaptivity)
	Setter of the parameter controlling the adaptive choice of the integration time step.
bool	setup (const Config::ParameterContainer &parameters, const std::string &prefix="")
	Method for setup of the explicit solver based on configuration parameters.
template<typename RHSFunction , typename... Args>
__cuda_callable__ bool	solve (VectorType &u, RHSFunction &&f, Args... args)
	Solve ODE given by a lambda function.
template<typename RHSFunction , typename... Args>
bool __cuda_callable__	solve (VectorType &u, RHSFunction &&rhsFunction, Args... args)
Public Member Functions inherited from TNL::Solvers::ODE::StaticExplicitSolver< Real, int >
__cuda_callable__	StaticExplicitSolver ()=default
	Default constructor.
bool __cuda_callable__	checkNextIteration ()
	Checks if the solver is allowed to do the next iteration.
__cuda_callable__ const RealType &	getMaxTau () const
	Getter of maximal value of the time step.
__cuda_callable__ const RealType &	getStopTime () const
	Getter of the time where the evolution computation shall by stopped.
__cuda_callable__ const RealType &	getTau () const
	Getter of the time step used for the computation.
__cuda_callable__ const RealType &	getTime () const
	Getter of the current time of the evolution computed by the solver.
__cuda_callable__ void	setMaxTau (const RealType &maxTau)
	Setter of maximal value of the time step.
__cuda_callable__ void	setStopTime (const RealType &stopTime)
	Setter of the time where the evolution computation shall by stopped.
__cuda_callable__ void	setTau (const RealType &tau)
	Setter of the time step used for the computation.
__cuda_callable__ void	setTestingMode (bool testingMode)
__cuda_callable__ void	setTime (const RealType &t)
	Settter of the current time of the evolution computed by the solver.
bool	setup (const Config::ParameterContainer &parameters, const std::string &prefix="")
	Method for setup of the iterative solver based on configuration parameters.
Public Member Functions inherited from TNL::Solvers::StaticIterativeSolver< Real, Index >
__cuda_callable__	StaticIterativeSolver ()=default
	Default constructor.
__cuda_callable__ bool	checkConvergence ()
	Checks whether the convergence occurred already.
__cuda_callable__ bool	checkNextIteration ()
	Checks if the solver is allowed to do the next iteration.
__cuda_callable__ const Real &	getConvergenceResidue () const
	Gets the the convergence threshold.
__cuda_callable__ const Real &	getDivergenceResidue () const
	Gets the limit for the divergence criterion.
__cuda_callable__ const Index &	getIterations () const
	Gets the number of iterations performed by the solver so far.
__cuda_callable__ const Index &	getMaxIterations () const
	Gets the maximal number of iterations the solver is allowed to perform.
__cuda_callable__ const Index &	getMinIterations () const
	Gets the minimal number of iterations the solver is supposed to do.
__cuda_callable__ const Real &	getResidue () const
	Gets the residue reached at the current iteration.
__cuda_callable__ bool	nextIteration ()
	Proceeds to the next iteration.
__cuda_callable__ void	resetIterations ()
	Sets the the number of the current iterations to zero.
__cuda_callable__ void	setConvergenceResidue (const Real &convergenceResidue)
	Sets the threshold for the convergence.
__cuda_callable__ void	setDivergenceResidue (const Real &divergenceResidue)
	Sets the residue limit for the divergence criterion.
__cuda_callable__ void	setMaxIterations (const Index &maxIterations)
	Sets the maximal number of iterations the solver is allowed to perform.
__cuda_callable__ void	setMinIterations (const Index &minIterations)
	Sets the minimal number of iterations the solver is supposed to do.
__cuda_callable__ void	setResidue (const Real &residue)
	Sets the residue reached at the current iteration.
bool	setup (const Config::ParameterContainer &parameters, const std::string &prefix="")
	Method for setup of the iterative solver based on configuration parameters.

Static Public Member Functions
static void	configSetup (Config::ConfigDescription &config, const std::string &prefix="")
	Static method for setup of configuration parameters.
Static Public Member Functions inherited from TNL::Solvers::ODE::StaticExplicitSolver< Real, int >
static void	configSetup (Config::ConfigDescription &config, const std::string &prefix="")
	This method defines configuration entries for setup of the iterative solver.
Static Public Member Functions inherited from TNL::Solvers::StaticIterativeSolver< Real, Index >
static void	configSetup (Config::ConfigDescription &config, const std::string &prefix="")
	This method defines configuration entries for setup of the iterative solver.

Static Public Attributes
static constexpr int	Size = Size_
	Size of the ODE system.

Protected Attributes
RealType	adaptivity = 0.00001
DofVectorType	k1
DofVectorType	k2
DofVectorType	k3
DofVectorType	k4
DofVectorType	k5
DofVectorType	kAux
Protected Attributes inherited from TNL::Solvers::ODE::StaticExplicitSolver< Real, int >
RealType	maxTau
bool	stopOnSteadyState
RealType	stopTime
RealType	tau
bool	testingMode
RealType	time
Protected Attributes inherited from TNL::Solvers::StaticIterativeSolver< Real, Index >
Real	convergenceResidue = 1e-6
Index	currentIteration = 0
Real	currentResidue = 0
Real	divergenceResidue = std::numeric_limits< Real >::max()
Index	maxIterations = 1000000000
Index	minIterations = 0
Index	refreshRate = 1

Detailed Description

template<int Size_, class Real>
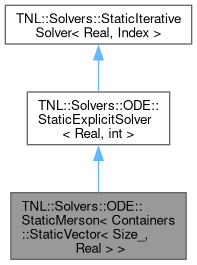
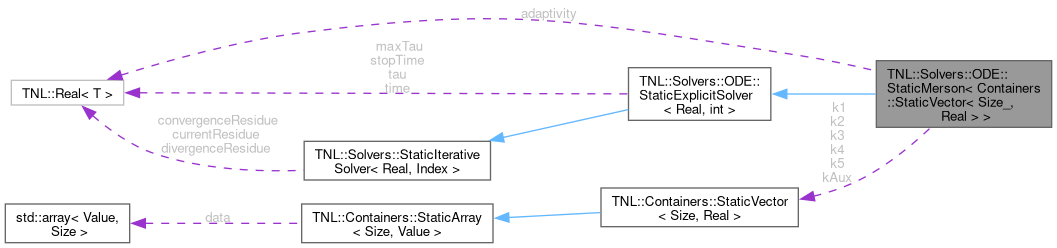
class TNL::Solvers::ODE::StaticMerson< Containers::StaticVector< Size_, Real > >

Solver of ODEs with the first order of accuracy.

This solver is based on the Runge-Kutta-Merson method with adaptive choice of the integration time step for solving of ordinary differential equations having the following form:

\( \frac{d u}{dt} = f( t, u) \text{ on } (0,T) \)

\( u( 0 ) = u_{ini} \). It is supposed to be used when the unknown \( \vec x \in R^n \) is expressed by a Containers::StaticVector.

For problems where \( x\) is represented by floating-point number, see TNL::Solvers::ODE::StaticMerson. For problems where \( \vec x\) is represented by TNL::Containers::Vector or TNL::Containers::VectorView, see TNL::Solvers::ODE::Merson.

The following example demonstrates the use the solvers:

#include <iostream>
#include <TNL/Containers/StaticVector.h>
#include <TNL/Solvers/ODE/StaticEuler.h>
 
using Real = double;
 
int
main( int argc, char* argv[] )
{
   using Vector = TNL::Containers::StaticVector< 3, Real >;
   using ODESolver = TNL::Solvers::ODE::StaticEuler< Vector >;
   const Real final_t = 25.0;
   const Real tau = 0.001;
   const Real output_time_step = 0.01;
   const Real sigma = 10.0;
   const Real rho = 28.0;
   const Real beta = 8.0 / 3.0;
 
   ODESolver solver;
   solver.setTau( tau );
   solver.setTime( 0.0 );
   Vector u( 1.0, 2.0, 3.0 );
   while( solver.getTime() < final_t ) {
      solver.setStopTime( TNL::min( solver.getTime() + output_time_step, final_t ) );
      auto f = [ = ]( const Real& t, const Real& tau, const Vector& u, Vector& fu )
      {
         const Real& x = u[ 0 ];
         const Real& y = u[ 1 ];
         const Real& z = u[ 2 ];
         fu[ 0 ] = sigma * ( y - x );
         fu[ 1 ] = rho * x - y - x * z;
         fu[ 2 ] = -beta * z + x * y;
      };
      solver.solve( u, f );
      std::cout << u[ 0 ] << " " << u[ 1 ] << " " << u[ 2 ] << std::endl;
   }
}

Since this variant of the Euler solver is static, it can be used even inside of GPU kernels and so combined with TNL::Algorithms::parallelFor as demonstrated by the following example:

#include <iostream>
#include <fstream>
#include <TNL/Solvers/ODE/StaticEuler.h>
#include <TNL/Containers/Vector.h>
#include <TNL/Algorithms/parallelFor.h>
#include <TNL/Containers/StaticArray.h>
 
using Real = double;
using MultiIndex = TNL::Containers::StaticArray< 3, int >;
 
template< typename Device >
void
solveParallelODEs( const char* file_name )
{
   using Vector = TNL::Containers::StaticVector< 3, Real >;
   using ODESolver = TNL::Solvers::ODE::StaticEuler< Vector >;
   const Real final_t = 50.0;
   const Real tau = 0.001;
   const Real output_time_step = 0.005;
   const Real sigma_min( 10.0 ), rho_min( 15.0 ), beta_min( 1.0 );
   const int parametric_steps = 4;
   const Real sigma_step = 30.0 / ( parametric_steps - 1 );
   const Real rho_step = 21.0 / ( parametric_steps - 1 );
   const Real beta_step = 15.0 / ( parametric_steps - 1 );
   const int output_time_steps = ceil( final_t / output_time_step ) + 1;
 
   const int results_size( output_time_steps * parametric_steps * parametric_steps * parametric_steps );
   TNL::Containers::Vector< Vector, Device > results( results_size, 0.0 );
   auto results_view = results.getView();
   auto f = [ = ] __cuda_callable__( const Real& t,
                                     const Real& tau,
                                     const Vector& u,
                                     Vector& fu,
                                     const Real& sigma_i,
                                     const Real& rho_j,
                                     const Real& beta_k )
   {
      const Real& x = u[ 0 ];
      const Real& y = u[ 1 ];
      const Real& z = u[ 2 ];
      fu[ 0 ] = sigma_i * ( y - x );
      fu[ 1 ] = rho_j * x - y - x * z;
      fu[ 2 ] = -beta_k * z + x * y;
   };
   auto solve = [ = ] __cuda_callable__( const MultiIndex& i ) mutable
   {
      const Real sigma_i = sigma_min + i[ 0 ] * sigma_step;
      const Real rho_j = rho_min + i[ 1 ] * rho_step;
      const Real beta_k = beta_min + i[ 2 ] * beta_step;
 
      ODESolver solver;
      solver.setTau( tau );
      solver.setTime( 0.0 );
      Vector u( 1.0, 1.0, 1.0 );
      int time_step( 1 );
      results_view[ ( i[ 0 ] * parametric_steps + i[ 1 ] ) * parametric_steps + i[ 2 ] ] = u;
      while( time_step < output_time_steps ) {
         solver.setStopTime( TNL::min( solver.getTime() + output_time_step, final_t ) );
         solver.solve( u, f, sigma_i, rho_j, beta_k );
         const int idx =
            ( ( time_step++ * parametric_steps + i[ 0 ] ) * parametric_steps + i[ 1 ] ) * parametric_steps + i[ 2 ];
         results_view[ idx ] = u;
      }
   };
   const MultiIndex begin = { 0, 0, 0 };
   const MultiIndex end = { parametric_steps, parametric_steps, parametric_steps };
   TNL::Algorithms::parallelFor< Device >( begin, end, solve );
 
   std::fstream file;
   file.open( file_name, std::ios::out );
   for( int sigma_idx = 0; sigma_idx < parametric_steps; sigma_idx++ )
      for( int rho_idx = 0; rho_idx < parametric_steps; rho_idx++ )
         for( int beta_idx = 0; beta_idx < parametric_steps; beta_idx++ ) {
            Real sigma = sigma_min + sigma_idx * sigma_step;
            Real rho = rho_min + rho_idx * rho_step;
            Real beta = beta_min + beta_idx * beta_step;
            file << "# sigma " << sigma << " rho " << rho << " beta " << beta << std::endl;
            for( int i = 0; i < output_time_steps - 1; i++ ) {
               int offset = ( ( i * parametric_steps + sigma_idx ) * parametric_steps + rho_idx ) * parametric_steps + beta_idx;
               auto u = results.getElement( offset );
               file << u[ 0 ] << " " << u[ 1 ] << " " << u[ 2 ] << std::endl;
            }
            file << std::endl;
         }
}
 
int
main( int argc, char* argv[] )
{
   TNL::String file_name( argv[ 1 ] );
   file_name += "/StaticODESolver-LorenzParallelExample-result.out";
 
   solveParallelODEs< TNL::Devices::Host >( file_name.getString() );
#ifdef __CUDACC__
   solveParallelODEs< TNL::Devices::Cuda >( file_name.getString() );
#endif
}

Template Parameters

Size	is size of the ODE system.
Real	is floating point number type, it is type of \( x \) in this case.

Member Function Documentation

configSetup()

template<int Size_, typename Real >

void TNL::Solvers::ODE::StaticMerson< Containers::StaticVector< Size_, Real > >::configSetup ( Config::ConfigDescription & config, const std::string & prefix = "" )

static

Static method for setup of configuration parameters.

Parameters

config	is the config description.
prefix	is the prefix of the configuration parameters for this solver.

getAdaptivity()

template<int Size_, typename Real >

__cuda_callable__ const Real & TNL::Solvers::ODE::StaticMerson< Containers::StaticVector< Size_, Real > >::getAdaptivity

(

)

const

Getter of the parameter controlling the adaptive choice of the integration time step.

Returns

the current value of the parameter controlling the adaptive choice of integration time step.

setAdaptivity()

template<int Size_, typename Real >

void __cuda_callable__ TNL::Solvers::ODE::StaticMerson< Containers::StaticVector< Size_, Real > >::setAdaptivity

(

const RealType &

adaptivity

)

Setter of the parameter controlling the adaptive choice of the integration time step.

The smaller the parammeter is the smaller the intergation time step tends to be. Reasonable values for this parameters are approximately from interval \( [10^{-12},10^{-2}] \).

Parameters

adaptivity

new value of the parameter controlling the adaptive choice of integration time step.

setup()

template<int Size_, typename Real >

bool TNL::Solvers::ODE::StaticMerson< Containers::StaticVector< Size_, Real > >::setup	(	const Config::ParameterContainer &	parameters,
		const std::string &	prefix = "" )

Method for setup of the explicit solver based on configuration parameters.

Parameters

parameters	is the container for configuration parameters.
prefix	is the prefix of the configuration parameters for this solver.

Returns

true if the parameters where parsed successfully.

false if the method did not succeed to read the configuration parameters.

solve()

template<int Size_, class Real >

template<typename RHSFunction , typename... Args>

__cuda_callable__ bool TNL::Solvers::ODE::StaticMerson< Containers::StaticVector< Size_, Real > >::solve	(	VectorType &	u,
		RHSFunction &&	f,
		Args...	args )

Solve ODE given by a lambda function.

Template Parameters

RHSFunction

is type of a lambda function representing the right-hand side of the ODE system. The definition of the lambda function reads as: auto f = [=] ( const Real& t, const Real& tau, const VectorType& u, VectorType& fu, Args... args ) {...} where t is the current time of the evolution, tau is the current time step, u is the solution at the current time, fu is variable/static vector into which the lambda function is suppsed to evaluate the function \( f(t, \vec x) \) at the current time \( t \).

Parameters

u	is a variable/static vector representing the solution of the ODE system at current time.
f	is the lambda function representing the right-hand side of the ODE system.
args	are user define arguments which are passed to the lambda function f.

Returns

true if steady state solution has been reached, false otherwise.

---

The documentation for this class was generated from the following files:

• src/TNL/Solvers/ODE/StaticMerson.h
• src/TNL/Solvers/ODE/StaticMerson.hpp