Template Numerical Library: TNL::Solvers::ODE::Euler< Vector, SolverMonitor

Solver of ODEs with the first order of accuracy. More...

#include <TNL/Solvers/ODE/Euler.h>

Inheritance diagram for TNL::Solvers::ODE::Euler< Vector, SolverMonitor >:

[legend]

Collaboration diagram for TNL::Solvers::ODE::Euler< Vector, SolverMonitor >:

[legend]

Public Types
using	DeviceType = typename Vector::DeviceType
	Device where the solver is supposed to be executed.

using	DofVectorType = TNL::Containers::Vector< RealType, DeviceType, IndexType >
	Alias for type of unknown variable \( \vec x \).

using	IndexType = typename Vector::IndexType
	Type for indexing.

using	RealType = typename Vector::RealType
	Type of floating-point arithemtics.

using	SolverMonitorType = SolverMonitor
	Type of object used for monitoring the convergence.

using	VectorType = Vector
	Type of unknown variable \( \vec x \).

Public Types inherited from TNL::Solvers::ODE::ExplicitSolver< Real, Index, SolverMonitor >
using	IndexType = Index
	Indexing type.

using	RealType = Real
	Type of the floating-point arithmetics.

using	SolverMonitorType = SolverMonitor
	Type of the monitor of the convergence of the solver.

Public Types inherited from TNL::Solvers::IterativeSolver< Real, Index, SolverMonitor >
using	SolverMonitorType = SolverMonitor
	Type of an object used for monitoring of the convergence.

Public Member Functions
	Euler ()=default
	Default constructor.

const RealType &	getCourantNumber () const
	Getter for the Courant number.

void	setCourantNumber (const RealType &c)
	This method sets the Courant number in the CFL condition.

bool	setup (const Config::ParameterContainer &parameters, const std::string &prefix="")
	Method for setup of the explicit solver based on configuration parameters.

template<typename RHSFunction >
bool	solve (VectorType &u, RHSFunction &&f)
	Solve ODE given by a lambda function.

Public Member Functions inherited from TNL::Solvers::ODE::ExplicitSolver< Real, Index, SolverMonitor >
	ExplicitSolver ()=default
	Default constructor.

bool	checkNextIteration ()
	Checks if the solver is allowed to do the next iteration.

const RealType &	getMaxTau () const
	Getter of maximal value of the time step.

const RealType &	getStopTime () const
	Getter of the time where the evolution computation shall by stopped.

const RealType &	getTau () const
	Getter of the time step used for the computation.

const RealType &	getTime () const
	Getter of the current time of the evolution computed by the solver.

void	refreshSolverMonitor (bool force=false)
	This method refreshes the solver monitor.

void	setMaxTau (const RealType &maxTau)
	Setter of maximal value of the time step.

void	setStopTime (const RealType &stopTime)
	Setter of the time where the evolution computation shall by stopped.

void	setTau (const RealType &tau)
	Setter of the time step used for the computation.

void	setTestingMode (bool testingMode)

void	setTime (const RealType &t)
	Settter of the current time of the evolution computed by the solver.

bool	setup (const Config::ParameterContainer &parameters, const std::string &prefix="")
	Method for setup of the iterative solver based on configuration parameters.

Public Member Functions inherited from TNL::Solvers::IterativeSolver< Real, Index, SolverMonitor >
	IterativeSolver ()=default
	Default constructor.

bool	checkConvergence ()
	Checks whether the convergence occurred already.

bool	checkNextIteration ()
	Checks if the solver is allowed to do the next iteration.

const Real &	getConvergenceResidue () const
	Gets the the convergence threshold.

const Real &	getDivergenceResidue () const
	Gets the limit for the divergence criterion.

const Index &	getIterations () const
	Gets the number of iterations performed by the solver so far.

const Index &	getMaxIterations () const
	Gets the maximal number of iterations the solver is allowed to perform.

const Index &	getMinIterations () const
	Gets the minimal number of iterations the solver is supposed to do.

const Real &	getResidue () const
	Gets the residue reached at the current iteration.

bool	nextIteration ()
	Proceeds to the next iteration.

void	resetIterations ()
	Sets the the number of the current iterations to zero.

void	setConvergenceResidue (const Real &convergenceResidue)
	Sets the threshold for the convergence.

void	setDivergenceResidue (const Real &divergenceResidue)
	Sets the residue limit for the divergence criterion.

void	setMaxIterations (const Index &maxIterations)
	Sets the maximal number of iterations the solver is allowed to perform.

void	setMinIterations (const Index &minIterations)
	Sets the minimal number of iterations the solver is supposed to do.

void	setRefreshRate (const Index &refreshRate)
	Sets the refresh rate (in milliseconds) for the solver monitor.

void	setResidue (const Real &residue)
	Sets the residue reached at the current iteration.

void	setSolverMonitor (SolverMonitorType &solverMonitor)
	Sets the solver monitor object.

bool	setup (const Config::ParameterContainer &parameters, const std::string &prefix="")
	Method for setup of the iterative solver based on configuration parameters.

Static Public Member Functions
static void	configSetup (Config::ConfigDescription &config, const std::string &prefix="")
	Static method for setup of configuration parameters.

Static Public Member Functions inherited from TNL::Solvers::ODE::ExplicitSolver< Real, Index, SolverMonitor >
static void	configSetup (Config::ConfigDescription &config, const std::string &prefix="")
	This method defines configuration entries for setup of the iterative solver.

Static Public Member Functions inherited from TNL::Solvers::IterativeSolver< Real, Index, SolverMonitor >
static void	configSetup (Config::ConfigDescription &config, const std::string &prefix="")
	This method defines configuration entries for setup of the iterative solver.

Protected Attributes
DofVectorType	_k1

RealType	courantNumber = 0.0

Protected Attributes inherited from TNL::Solvers::ODE::ExplicitSolver< Real, Index, SolverMonitor >
RealType	maxTau = std::numeric_limits< RealType >::max()

bool	stopOnSteadyState = false

RealType	stopTime

RealType	tau = 0.0

bool	testingMode = false

RealType	time = 0.0

Protected Attributes inherited from TNL::Solvers::IterativeSolver< Real, Index, SolverMonitor >
Real	convergenceResidue = 1e-6

Index	currentIteration = 0

Real	currentResidue = 0

Real	divergenceResidue = std::numeric_limits< Real >::max()

Index	maxIterations = 1000000000

Index	minIterations = 0

Index	refreshRate = 1

std::ofstream	residualHistoryFile

std::string	residualHistoryFileName = ""

SolverMonitor *	solverMonitor = nullptr

Detailed Description

template<typename Vector, typename SolverMonitor = IterativeSolverMonitor< typename Vector::RealType, typename Vector::IndexType >>
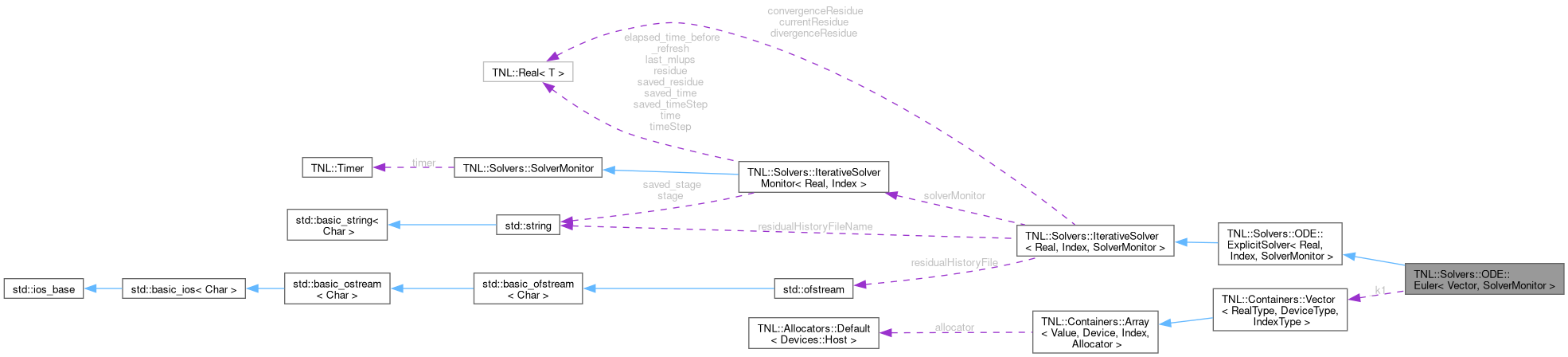
class TNL::Solvers::ODE::Euler< Vector, SolverMonitor >

Solver of ODEs with the first order of accuracy.

This solver is based on the Euler method for solving of ordinary differential equations having the following form:

\( \frac{d \vec u}{dt} = \vec f( t, \vec u) \text{ on } (0,T) \)

\( \vec u( 0 ) = \vec u_{ini} \).

It is supposed to be used when the unknown \( \vec x \in R^n \) is expressed by a Containers::Vector.

For problems where \( \vec x\) is represented by TNL::Containers::StaticVector, see TNL::Solvers::ODE::StaticEuler<Containers::StaticVector<Size_,Real>>. For problems where \( x\) is represented by floating-point number, see TNL::Solvers::ODE::StaticEuler.

The following example demonstrates the use the solvers:

#include <iostream>
#include <TNL/FileName.h>
#include <TNL/Containers/Vector.h>
#include <TNL/Solvers/ODE/Euler.h>
#include "write.h"
 
using Real = double;
using Index = int;
 
template< typename Device >
void
solveHeatEquation( const char* file_name )
{
   using Vector = TNL::Containers::Vector< Real, Device, Index >;
   using VectorView = typename Vector::ViewType;
   using ODESolver = TNL::Solvers::ODE::Euler< Vector >;
 
   /***
    * Parameters of the discretisation
    */
   const Real final_t = 0.05;
   const Real output_time_step = 0.005;
   const Index n = 41;
   const Real h = 1.0 / ( n - 1 );
   const Real tau = 0.1 * h * h;
   const Real h_sqr_inv = 1.0 / ( h * h );
 
   /***
    * Initial condition
    */
   Vector u( n );
   u.forAllElements(
      [ = ] __cuda_callable__( Index i, Real & value )
      {
         const Real x = i * h;
         if( x >= 0.4 && x <= 0.6 )
            value = 1.0;
         else
            value = 0.0;
      } );
   std::fstream file;
   file.open( file_name, std::ios::out );
   write( file, u, n, h, (Real) 0.0 );
 
   /***
    * Setup of the solver
    */
   ODESolver solver;
   solver.setTau( tau );
   solver.setTime( 0.0 );
 
   /***
    * Time loop
    */
   while( solver.getTime() < final_t ) {
      solver.setStopTime( TNL::min( solver.getTime() + output_time_step, final_t ) );
      auto f = [ = ] __cuda_callable__( Index i, const VectorView& u, VectorView& fu ) mutable
      {
         if( i == 0 || i == n - 1 )  // boundary nodes -> boundary conditions
            fu[ i ] = 0.0;
         else  // interior nodes -> approximation of the second derivative
            fu[ i ] = h_sqr_inv * ( u[ i - 1 ] - 2.0 * u[ i ] + u[ i + 1 ] );
      };
      auto time_stepping = [ = ]( const Real& t, const Real& tau, const VectorView& u, VectorView& fu )
      {
         TNL::Algorithms::parallelFor< Device >( 0, n, f, u, fu );
      };
      solver.solve( u, time_stepping );
      write( file, u, n, h, solver.getTime() );  // write the current state to a file
   }
}
 
int
main( int argc, char* argv[] )
{
   TNL::String file_name( argv[ 1 ] );
   file_name += "/ODESolver-HeatEquationExample-result.out";
 
   solveHeatEquation< TNL::Devices::Host >( file_name.getString() );
#ifdef __CUDACC__
   solveHeatEquation< TNL::Devices::Cuda >( file_name.getString() );
#endif
}

Template Parameters

Vector is type of vector storing \( \vec x \in R^n \), mostly TNL::Containers::Vector or TNL::Containers::VectorView.

Member Typedef Documentation

◆ DofVectorType

template<typename Vector , typename SolverMonitor = IterativeSolverMonitor< typename Vector::RealType, typename Vector::IndexType >>

using TNL::Solvers::ODE::Euler< Vector, SolverMonitor >::DofVectorType = TNL::Containers::Vector< RealType, DeviceType, IndexType >

Alias for type of unknown variable \( \vec x \).

Note that VectorType can be TNL::Containers::VectorView but DofVectorType is always TNL::Containers::Vector.

◆ SolverMonitorType

template<typename Vector , typename SolverMonitor = IterativeSolverMonitor< typename Vector::RealType, typename Vector::IndexType >>

using TNL::Solvers::ODE::Euler< Vector, SolverMonitor >::SolverMonitorType = SolverMonitor

Type of object used for monitoring the convergence.

Can be TNL::Solvers::IterativeSolverMonitor.

Member Function Documentation

◆ configSetup()

template<typename Vector , typename SolverMonitor >

void TNL::Solvers::ODE::Euler< Vector, SolverMonitor >::configSetup	(	Config::ConfigDescription &	config,
		const std::string &	prefix = "" )

static

Static method for setup of configuration parameters.

Parameters

config	is the config description.
prefix	is the prefix of the configuration parameters for this solver.

◆ getCourantNumber()

template<typename Vector , typename SolverMonitor >

auto TNL::Solvers::ODE::Euler< Vector, SolverMonitor >::getCourantNumber ( ) const

Getter for the Courant number.

Returns: the Courant number.

◆ setCourantNumber()

template<typename Vector , typename SolverMonitor >

void TNL::Solvers::ODE::Euler< Vector, SolverMonitor >::setCourantNumber ( const RealType & c )

This method sets the Courant number in the CFL condition.

This method sets the constant \( C \) in the Courant–Friedrichs–Lewy condition. It means that

\[ \Delta t = \frac{C}{\| f( t,x )\|}, \]

if \( C > 0\). If \( C = 0 \) the time step stays fixed.

Parameters

c	is the Courant number.

◆ setup()

template<typename Vector , typename SolverMonitor >

bool TNL::Solvers::ODE::Euler< Vector, SolverMonitor >::setup	(	const Config::ParameterContainer &	parameters,
		const std::string &	prefix = "" )

Method for setup of the explicit solver based on configuration parameters.

Parameters

parameters	is the container for configuration parameters.
prefix	is the prefix of the configuration parameters for this solver.

Returns: true if the parameters where parsed successfully.; false if the method did not succeed to read the configuration parameters.

◆ solve()

template<typename Vector , typename SolverMonitor >

template<typename RHSFunction >

bool TNL::Solvers::ODE::Euler< Vector, SolverMonitor >::solve	(	VectorType &	u,
		RHSFunction &&	f )

Solve ODE given by a lambda function.

Template Parameters

RHSFunction

is type of a lambda function representing the right-hand side of the ODE system. The definition of the lambda function reads as:

auto f = [=] ( const Real& t, const Real& tau, const VectorType& u, VectorType& fu ) {...}

TNL::Solvers::ODE::Euler::VectorType

Vector VectorType

Type of unknown variable .

Definition Euler.h:62

where t is the current time of the evolution, tau is the current time step, u is the solution at the current time, fu is variable/static vector into which the lambda function is suppsed to evaluate the function \( f(t, \vec x) \) at the current time \( t \).

Parameters

u	is a variable/static vector representing the solution of the ODE system at current time.
f	is the lambda function representing the right-hand side of the ODE system.

Returns: true if steady state solution has been reached, false otherwise.

The documentation for this class was generated from the following files:

src/TNL/Solvers/ODE/Euler.h
src/TNL/Solvers/ODE/Euler.hpp

Public Types

Public Member Functions

Static Public Member Functions

Protected Attributes

Detailed Description

Member Typedef Documentation

◆ DofVectorType

◆ SolverMonitorType

Member Function Documentation

◆ configSetup()

◆ getCourantNumber()

◆ setCourantNumber()

◆ setup()

◆ solve()